Analytical and Numerical Treatments of Conservative Diffusions and the Burgers Equation

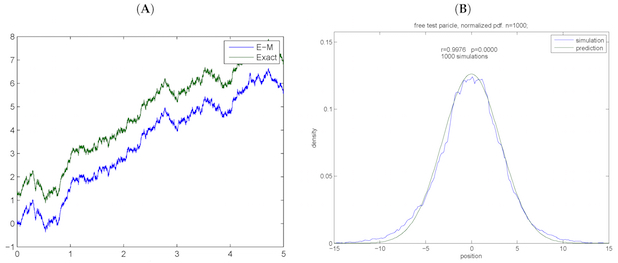
The present work is concerned with the study of a generalized Langevin equation and its link to the physical theories of statistical mechanics and scale relativity. It is demonstrated that the form of the coefficients of the Langevin equation depends critically on the assumption of continuity of the reconstructed trajectory. This in turn demands for the fluctuations of the diffusion term to be discontinuous in time. This paper further investigates the connection between the scale-relativistic and stochastic mechanics approaches, respectively, with the study of the Burgers equation, which in this case appears as a stochastic geodesic equation for the drift. By further demanding time reversibility of the drift, the Langevin equation can also describe equivalent quantum-mechanical systems in a path-wise manner. The resulting statistical description obeys the Fokker–Planck equation of the probability density of the differential system, which can be readily estimated from simulations of the random paths. Based on the Fokker–Planck formalism, a new derivation of the transient probability densities is presented. Finally, stochastic simulations are compared to the theoretical results. View Full-Text / Download Paper

By Dimiter Prodanov



This abstract belongs to an article of the Special Issue "Emergent Quantum Mechanics – David Bohm Centennial Perspectives"



Visit EmQM17 symposium page